A minap, mikor már sokadszorra bukkant fel a Planck-állandó a képletekben tanulás során, meg kellett kérdeznem, mennyi is az pontosan. Arra emlékeztem, hogy egy pici szám, de amikor szembesültem a 6,626∙10^-34 Js-mal, megállapítottam, hogy az bizony nagyon nagyon pici. Nem is tudom semmihez sem viszonyítani. A hatványokkal sokszor előfordul ez a helyzet, amikor valami nagyon kis vagy éppen nagy számot csak úgy mondunk, vagy hallunk.

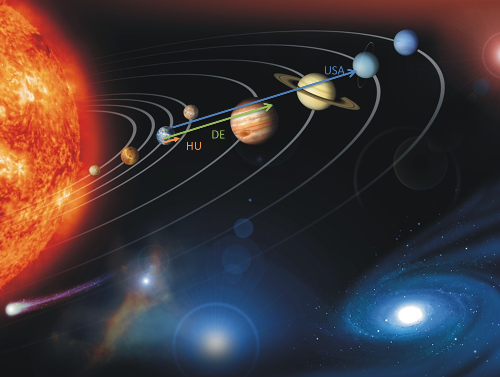
Talán a legtöbbször az zavar, amikor egy nagyobb ország költségvetésével kapcsolatban sok milliárd dollárokat emlegetnek. Az sok pénz, méghozzá olyan sok, hogy nem is tudom felfogni. Valami kézzelfogható kell, amihez viszonyíthatok. Egy ház ára körülbelül a legmagasabb érték, amit felfoghatónak érzek, aztán még el tudok képzelni sok háznyi értéket, meg sok házat a tengerparton, stb. Mégis, valahogy ezek sincsenek rendben. Mennyi is az a több mint 2300 milliárd USD, ami például az USA költségvetése? Az pontosan 2,3∙10¹² USD. Ez valamivel kevesebb, mint Magyarország költségvetése forintban, de nem hiszem, hogy ezzel már megvilágítottam a 10¹² nagyságát. Rugaszkodjunk el a pénzvilágtól, és gondolkodjunk időben. Ha már az idő pénz, váltsuk a USD-t másodpercre! 2,3∙ 10¹² sec=72932.5 év (amihez szintén viszonyításnak: kb. 90000 éve létezik a Homo sapiens, és kb 40000 évvel ezelőttre teszik, hogy elterjedt Eurázsia területén). De feltehetjük azt a kérdést is, hogy kinek meddig ér a takarója? Váltsuk át gondolatban a dollárokat méterre! 2,3∙ 10¹² m azzal átlagosan elérnek az Uránuszig, míg hazánk 74 milliárdjával a Mars pályáját is csak jól megválasztott napokon érintenénk (nem koncentrikus körpályákról lévén szó), egy középosztálybeli család pedig az Egyenlítőt (40000 km) sem kerüli meg - jól illusztrálva, hogy világkörüli utazásról sem nagyon álmodhat, legfeljebb csak a sarkkörök környékén.

Máshol is találkozhatunk nagy számokkal, például az általános iskolában is hallhatunk már az Avogadro-számról, ami 6∙10²³ darab részecskét jelent. Ez tesz ki pontosan 1 mólnyi anyagot, vagyis például 18 g vizet, vagy 56 g vasat. A tömeg alapján az nem is olyan sok, bezzeg részecskében mérve! Ha az előbbi módszerrel élünk, akkor 3.17∙10¹⁵ évre válthatjuk a másodperceket, amit a födtörténeti korok mesélésekor sem tudunk elhelyezni, sőt az univerzum korát is meghaladtuk, mert az is „csak” 13,77 milliárd (13,77∙10⁹) éves. Szóval megbuktunk az időskálán történő viszonyításunkkal. Nézzük meg, a dolog talán jobban működik távolsággal szemléltetve. 6∙10²³ m-t átválthatjuk máris fényévre, hogy a lehető legnagyobb mértékegységgel éljünk, amit használunk, ez pedig kb. 60 millió fényév, vagyis a hozzánk legközelebbi galaxishalmaz távolsága (Virgo-halmaz), ami csillagainak fényét 60 millió év késéssel láthatjuk itt a Földön. ...Őszintén szólva, megint egy felfoghatatlan adat, amit leírtam, ez egyszerűen túl nagy! Még egy lehetőség: próbáljuk meg, hogy az egy mólnyi atomot képzeletben egyszerűen sorba állítjuk hézagmentesen egy hosszú láncot formálva (ez persze fizikailag lehetetlen, de ezért jó a gondolatkísérlet)! Vegyük a legkisebb atomot, a hidrogént! Tudjuk, hogy egy hidrogén atom átmérője kb. 50 pm, azaz 5∙10^-11 m. Ha veszünk egy mólnyi atomot, akkor az sorba rakva egy láthatatlan, több mint 3∙10¹³ m-es láncot alkotna, ami körbeérne a Plútó pályáján, és a fénynek több mint egy napig tartana elérni az egyik végétől a másikra.

És ezzel át is térhetünk a kis számokra, mint az előbb említett pm (piko: 10^-12) vagy a sokat emlegetett nanotechnológia kapcsán a nano (10^-9) léptékekre. A nanorészecskéknél maradva képzeljük el a mm egymilliomod részét! – ugye nem megy? Nanométeres dimenziókba már egész nagy molekulák beleférnek. Ilyen molekulákból épülhet fel az a legkisebb méretű szösz, ami éppen az olvasó monitorára tapad, és már szabad szemmel látható. Ha jó az olvasó szeme, vagy feltette a szemüvegét, ez a kis szösz körülbelül 100 m (mikrométer=10^-6 m), azaz 10^-4 m. Ha ez a szösz lenne a molekula, ami felépíti, a szösz maga legalább két dimenziójában 10 méteres lenne.

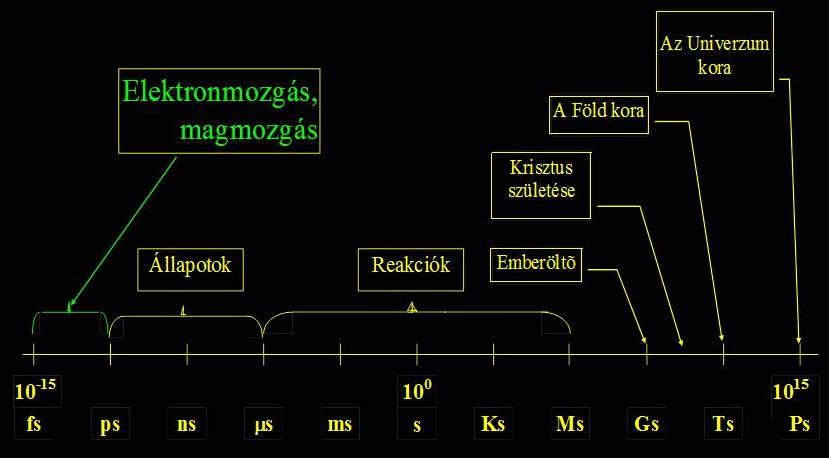
Kis számokkal még az időmérés során találkozunk. A gyorsasági versenyeken teljesen általános, hogy ezred másodperceket (ms) mérnek. Ha az 1 ms nem is, a nem sokkal több már a nézőnek is teljesen jól érzékelhető, de mi a helyzet a kisebb egységekkel? Mindenki találkozott már lézerekkel, azt viszont nem mindenki tudja, hogy nagyon sok féle lézer létezik, és tulajdonságaiktól függően nagyon sok kutatásban tudják alkalmazni őket. Egyik legfontosabb alkalmazása az impulzus üzemű lázereknek a különböző kémiai folyamatok lefutásának vizsgálata. Egy kémiai folyamat lehet nagyon lassú, de nagyon gyors is. A leggyorsabb folyamat, amit ma vizsgálni tudnak (akár sejtekben is), fs (femto=10^-15) nagyságrendű. Ilyen folyamat például, amikor egy fluoreszkáló anyag fényt bocsát ki. A fényjelenség annak következménye, hogy egy elektron a lézerfény hatására ugrik egyet, és magasabb energiájú lesz, majd onnan visszakerül alapállapotba. A folyamat első lépése a leggyorsabb, 10^-15 s körüli, majd ehhez képest lassan történik némi átrendeződés (ps), végül visszaugrik az elektron az – eredeti – alapállapotába egy ns (10^-9 s) alatt. Ha mondjuk ez az elektron megnézne, amikor ugrok egyet, hogy lássam, mi van a boltban a felső polcon, tegyük fel, egy másodperc alatt (ez mondjuk egy komolyabb kosaras karriert feltételezne, mert 1,25 méteres emelkedéshez kell ennyi idő), azt neki a megszokott mozgáskultúrájával olyan lassú lenne kivárni, mint nekem a világ jelen állapotát az ősrobbanástól fogva.

Az atomokat alkotó kisebb építőegységek tömegét is ismerjük. Például a proton tömege 1,67∙10^-24 g. Ha történetesen a „Drágám, a kölykök összementek”-ben a gyerekek ilyen méretűre mentek volna össze, akkor egy kis - ám az ő perspektívájukból nézve roppant ijesztő – darázs nekik az Élő Bolygót (6∙10²⁷ g) jelentette volna - legalábbis ami a tömegarányokat illeti.

Bizonyos dolgokat nehéz ténylegesen értelmezni. A matematika ezekre kitalált módszereket, hogy legalább leírni tudjuk. Így dolgozunk hatványokkal, logaritmikus skálán vagy sokdimenziós vektorokkal. Néha azonban megéri megmozgatni a fantáziánkat és elképzelni, mi is rejlik a számok mögött, vagy egyszerűen elszórakozni a gondolattal, hogy mi lenne, ha olyan gyorsak lehetnénk, mint a fény, vagy vagy csak tudnánk valami olyat csinálni, ami akkora lenne, mint...