31. A tömeg eredete és a Higgs-mező (Dávid Gyula előadása)
„A Higgs-mező – sőt, a nevének az említése - tömeget generál.”
-Dávid Gyula-
A fenti idézettel kezdte szeptember 13-án „A tömeg eredete és a Higgs-mező” című előadását Dávid Gyula az ELTE „Az atomoktól a csillagokig” elnevezésű, egész éven át tartó rendezvénysorozata keretében (melyről többet az előző írásban tudhattatok meg) a téma okán zsúfolásig megtelt teremben. A nagyszerű szervezésnek és honlapnak köszönhetően nem csak az előadás fóliái tölthetőek le, de a kifogástalan minőségű videó felvétel is. Utóbbit bátorkodtunk közzétenni a Youtube-on, hogy minden olvasó maga is megtekinthesse.
 A „Mire 'jó' a Higgs-bozon?” című írás – szintén Dávid Gyula klaviatúrájából kölcsönözve - máig a legolvasottabb bejegyzés ezeken a hasábokon, melyet a nagy érdeklődésre való tekintettel követett a részecskék igen bő világának kis rendszerezése, betekintést engedve a proton-neutron-elektron triumvirátus mögött megbújó hihetetlen világba. Már az utóbbi cikkben beígértük a Higgs-bozonról szóló részletesebb tájékoztatást, így majd 3 hónap elteltével eljött ez a pillanat is. A rendkívül élvezetes, DGY-hez méltóan sodró lendületű előadáshoz nem nagyon lehet mit hozzátenni, így nem is kísérelnénk meg. Mindenkinek csak ajánlani tudjuk az alább beágyazott videó megtekintését, melynek rövid kivonatát megpróbáltuk összefoglalni a prezentált fóliák segítségével. Tovább után következik Dávid Gyula előadásának interpretációja és a Higgs-mező tengerén hánykolódó hajók!
A „Mire 'jó' a Higgs-bozon?” című írás – szintén Dávid Gyula klaviatúrájából kölcsönözve - máig a legolvasottabb bejegyzés ezeken a hasábokon, melyet a nagy érdeklődésre való tekintettel követett a részecskék igen bő világának kis rendszerezése, betekintést engedve a proton-neutron-elektron triumvirátus mögött megbújó hihetetlen világba. Már az utóbbi cikkben beígértük a Higgs-bozonról szóló részletesebb tájékoztatást, így majd 3 hónap elteltével eljött ez a pillanat is. A rendkívül élvezetes, DGY-hez méltóan sodró lendületű előadáshoz nem nagyon lehet mit hozzátenni, így nem is kísérelnénk meg. Mindenkinek csak ajánlani tudjuk az alább beágyazott videó megtekintését, melynek rövid kivonatát megpróbáltuk összefoglalni a prezentált fóliák segítségével. Tovább után következik Dávid Gyula előadásának interpretációja és a Higgs-mező tengerén hánykolódó hajók!
A nagy felfedezéssel kapcsolatban számtalanszor elhangzott, hogy ezzel helyére került a részecskefizika standard modelljének utolsó hiányzó építőkockája is. Legtöbbször kiemelik azt is, hogy a Higgs-részecske speciális szerepet tölt be, ugyanis ő ad tömeget a többi részecskének. Itt máris meg kell álljunk, és az egyszerűnek tűnő szavak mögé kell pillantanunk. Mi az, hogy tömeget AD a részecskéknek? Hogy lehet tömeget adni? Sőt, ha jobban belegondolunk: mi is az a tömeg?
Visszakanyarodva a középiskolás időkbe egy relatíve egyszerű választ adhatunk az utolsó kérdésre: azt szoktuk mondani, hogy a tömeg az anyagmennyiség (vagy a tehetetlenség) mértéke. Természetesnek vettük, hogy értéke állandó, és minden objektum rendelkezik vele. Komplikáltabbá válik az élet a modern fizika jelenségeit vizsgálva, ugyanis a relativitáselmélet kimondja: a tömeg a nyugvó test energiája. Hogy mihez képest nyugszik egy test, azt a relativitáselmélet tárgyalja (részletek: 2009. január 15. - Dávid Gyula: Relativisztikus paradoxonok). Már ez a megfogalmazás is magában rejti, hogy a gyorsabban mozgó testek több energiával rendelkeznek és lendületük is nagyobb. Mit mondhatunk az álló testről? Lendülete nyilvánvalóan nincsen, míg az energia már egy nehezebb kérdés: a klasszikus fizika szerint nincs, a relativitáselmélet szerint van. Ábrázoljuk a kapcsolatot a lendület és az energia közt:
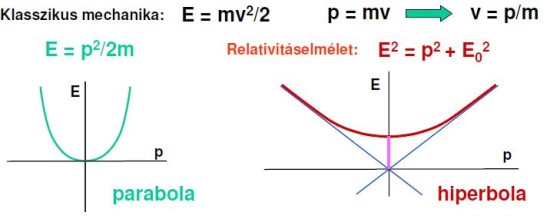
Két alapjaiban különböző ábrát kapunk első ránézésre. Newton ekkorát tévedett volna? A válasz: nem! Nézzük más perspektívából a két görbét, úgy is mondhatnánk, hogy kicsit messzebbről, és toljuk el a parabola 0 energiaszintjét (a 0 megválasztása önkényes, ezt mindenki tapasztalhatta már középiskolában a helyzeti energia számolásakor, nem kell mindig a Föld középpontjához viszonyítani ott sem).
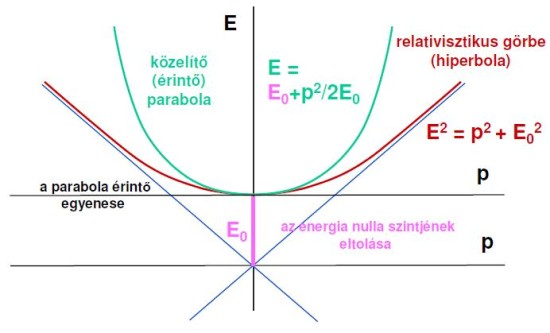
Ha a p=0 pont környezetében nézelődünk (alacsony sebességek), akkor azt láthatjuk, hogy a két különböző görbe itt bizony roppant hasonlóan viselkedik. Mivel Newton lehulló almákkal foglalkozott nem pedig felgyorsított protonokkal, így esetében nem beszélhetünk „nagy” tévedésről, birodalmában a két görbe gyakorlatilag észrevehetetlen különbségeket mutat csak. Ha ezek után összeillesztjük a kapott formulákat, akkor egy meglepő következtetésre juthatunk: a két leírás úgy lesz konzisztens egymással, ha a nyugalmi energia megegyezik a test tömegével! Pontosabban ha a nyugalmi energia megegyezik a tömeg szorozva a fénysebesség négyzetével. Utóbbi korrekcióra azért van szükség, mert elődjeink a természet leírására tett igyekezetek közepette rosszul választottak mértékegységeket, így később be kellett vezetni egy átváltási tényezőt, a jól ismert c-t - a modern fizikában ezt szokás egységnyinek tekinteni a formulák egyszerűsítése végett. Nem tudhatták még, hogy az energiát, a tömeget és az impulzust egyfajta mértékegységgel kell mérni. (Meg arról se feledkezzünk meg, hogy az „E egyenlő m c négyzet” mennyivel jobban hangzik, mint a sima E=m. Utóbbit mégsem lehet csak úgy pólókra írni...)
Mit mondhatunk a különböző tömegű részecskékről?
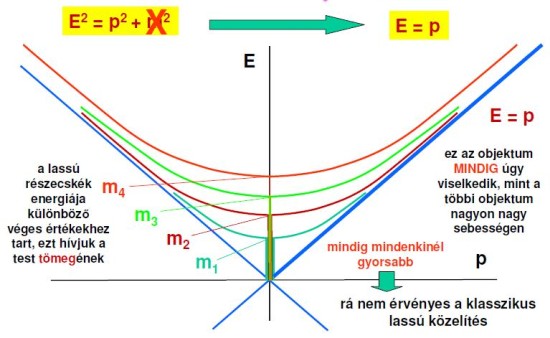
Amint az ábrán láthatjuk, igen nagy p értékek mellett a tömeg elhanyagolhatóvá válik, és az összes részecske hasonlóan viselkedik, ugyanahhoz az egyeneshez tart minden görbe. Az is leolvasható, hogy ha m=0, akkor az ehhez az esethez tartozó részecske minden sebesség mellett úgy viselkedik mint az összes többi a nagy p határesetben. Ilyen részecske létezik is: ez a mindenki által ismert foton. Ennek nincs a klasszikus fizika által kezelhető leírása, nem létezik „lassú közelítése”. A részecskék döntő többsége azonban nem ilyen. Ezzel az a probléma, hogy a kvantum-mezőelmélet (QFT) csak a 0 nyugalmi tömegű részecskéket tudja jól leírni. Erre a kérdésre később még vissza fogunk térni, most azonban gondolkodjunk el kicsit a kölcsönhatásokról.
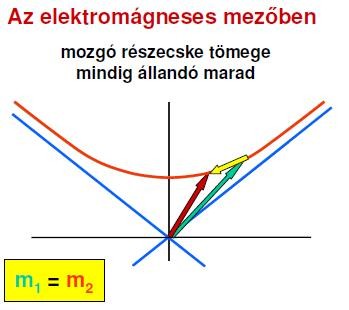 Ha a hiperboláinkra nézünk, akkor láthatjuk, hogy minden tömeghez más-más hiperbola tartozik. Egy kölcsönhatás leírható a test impulzusának és energiájának megváltozásával, így azt gondolhatnánk, hogy a p-E térképünkön tetszőleges módon elmozdulhatunk. Ez azonban azt jelentené, hogy az esetek nagy többségében másik hiperbolára kerülnénk (sokkal több olyan nyilat húzhatunk, amelynek két végpontja más-más görbén van), ami egyenértékű azzal, hogy megváltozna a test tömege. Mégsem ezt tapasztaljuk. Ennek oka, hogy a világunkat uraló elektromágneses mező éppen olyan tulajdonságokkal rendelkezik, hogy a tömeget változatlanul hagyja, így a klasszikus leírásmód során nem jött elő a probléma.
Ha a hiperboláinkra nézünk, akkor láthatjuk, hogy minden tömeghez más-más hiperbola tartozik. Egy kölcsönhatás leírható a test impulzusának és energiájának megváltozásával, így azt gondolhatnánk, hogy a p-E térképünkön tetszőleges módon elmozdulhatunk. Ez azonban azt jelentené, hogy az esetek nagy többségében másik hiperbolára kerülnénk (sokkal több olyan nyilat húzhatunk, amelynek két végpontja más-más görbén van), ami egyenértékű azzal, hogy megváltozna a test tömege. Mégsem ezt tapasztaljuk. Ennek oka, hogy a világunkat uraló elektromágneses mező éppen olyan tulajdonságokkal rendelkezik, hogy a tömeget változatlanul hagyja, így a klasszikus leírásmód során nem jött elő a probléma.
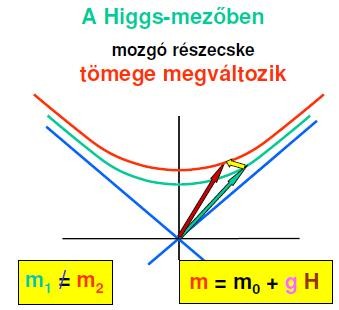 Létezik vajon más fajta mező is? Egyáltalán mi az a mező? A mező egy térben folytonos eloszlású mennyiség, mely a tér minden pontjához hozzárendel egy értéket. Ez az érték lehet egy vektor (például Magyarország széltérképe: minden pontban megadjuk a szél nagyságát és irányát) vagy egy skalár is (hőmérsékleti térkép). A Higgs-mező is egy ilyen skalármező, melynek értéke a tér minden pontjában a H Higgs-potenciállal jellemezhető. Ez a mező erőt gyakorol a vele kölcsönható testekre, a csatolási állandó az adott testre jellemző g mennyiség (ez adja meg az arányosságot az erő és a potenciál közt, hasonlóan a töltéshez, mely az elektromágneses tér által kifejtett erő meghatározásához szükséges: nagyobb töltésű testre ugyanaz a tér nagyobb erővel hat). A Higgs-mezőben mozgó részecske tömege már megváltozik az ábrán látható formulának megfelelően!
Létezik vajon más fajta mező is? Egyáltalán mi az a mező? A mező egy térben folytonos eloszlású mennyiség, mely a tér minden pontjához hozzárendel egy értéket. Ez az érték lehet egy vektor (például Magyarország széltérképe: minden pontban megadjuk a szél nagyságát és irányát) vagy egy skalár is (hőmérsékleti térkép). A Higgs-mező is egy ilyen skalármező, melynek értéke a tér minden pontjában a H Higgs-potenciállal jellemezhető. Ez a mező erőt gyakorol a vele kölcsönható testekre, a csatolási állandó az adott testre jellemző g mennyiség (ez adja meg az arányosságot az erő és a potenciál közt, hasonlóan a töltéshez, mely az elektromágneses tér által kifejtett erő meghatározásához szükséges: nagyobb töltésű testre ugyanaz a tér nagyobb erővel hat). A Higgs-mezőben mozgó részecske tömege már megváltozik az ábrán látható formulának megfelelően!
 Érdemes megjegyezni, hogy ezt a formulát már 1953-ban levezette Novobátzky Károly, az ELTE TTK Elméleti Fizika Tanszékének vezetője, valamint Marx György 1950 és 1955 közt részletesen kidolgozta a relativisztikus mechanika hiányzó fejezeteit, figyelembe véve a tömeg megváltozásának jelenségét. Sajnos a vasfüggöny következtében ez a hihetetlen hír nem jutott el a nyugati tudományos közvéleményhez, mely Peter Higgs-nek hála a 60-as években újra felfedezte a jelenséget, és azt számos részlettel kiegészítve megalkotta a standard modell alapkövéül szolgáló elméletet. A témáról további részletek megismerhetőek Veres Gábor (Milyen eszközökkel figyelhetőek meg a világ legkisebb alkotórészei?) és Varga Dezső (A legkisebb részecskék a világ legnagyobb gyorsítójában) előadásaiból.
Érdemes megjegyezni, hogy ezt a formulát már 1953-ban levezette Novobátzky Károly, az ELTE TTK Elméleti Fizika Tanszékének vezetője, valamint Marx György 1950 és 1955 közt részletesen kidolgozta a relativisztikus mechanika hiányzó fejezeteit, figyelembe véve a tömeg megváltozásának jelenségét. Sajnos a vasfüggöny következtében ez a hihetetlen hír nem jutott el a nyugati tudományos közvéleményhez, mely Peter Higgs-nek hála a 60-as években újra felfedezte a jelenséget, és azt számos részlettel kiegészítve megalkotta a standard modell alapkövéül szolgáló elméletet. A témáról további részletek megismerhetőek Veres Gábor (Milyen eszközökkel figyelhetőek meg a világ legkisebb alkotórészei?) és Varga Dezső (A legkisebb részecskék a világ legnagyobb gyorsítójában) előadásaiból.
Értsük meg a tömegadást matek nélkül!
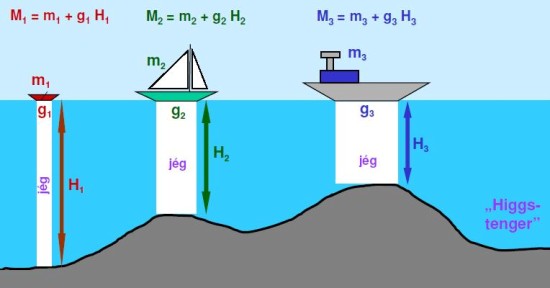
Képzeljük el a részecskéket úgy, mint a Higgs-tengeren úszkáló hajókat. A hajóink hidegek, ezért mindegyik aljára odafagy egy jégoszlop, mely a tengerfenékig ér. Értelemszerűen minél több jeget cipel egy adott hajó, annál nehezebb lesz, a jég tömege hozzáadódik a hajó saját tömegéhez (m). A tenger mélysége megfelel a Higgs-potenciál értékének, a hajó fenekének nagysága pedig a g csatolási állandónak.
Nyilvánvaló, hogy ha egy hajó arrébb megy, akkor változik a jégoszlop magassága, ezáltal a tömeg is. Ezt azonban nem tapasztaljuk a valóságban. A részecskék tömege éppen ugyanannyi a bejárati ajtónál és az ebédlőasztal mellett is. Higgs kimutatta, hogy ez valóban így van, a „Higgs-tenger állandó mélységű”, szerencsénkre egy kotróhajó az univerzum évmilliárdjai során kisimította a tengerfeneket (az óceán az Ősrobbanás idején igencsak háborgott még...), így mozgás közben nem változik a tömeg. Kiszámolta továbbá azt is, hogy a hajók nyugalmi tömege 0. Ez azért örömteli, mert mindez konzisztens a QFT korábban említett eredményeivel!
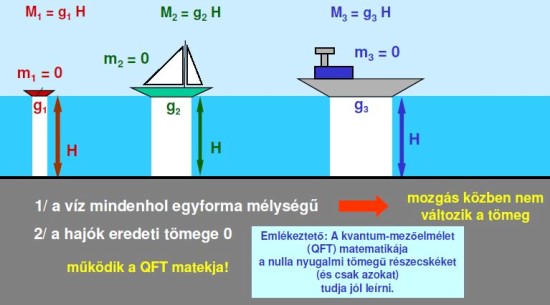
Egy kérdés maradt csak hátra – már ami egy szemléltető, bevezető előadás anyagába beleférhet -: miért nem láttuk ezt eddig? Azért, mert a „Higgs-víz” és a „Higgs-jég” is láthatatlan. Két részecske – hajó – nagy energiájú ütközésekor az alábbi jelenség játszódik le:
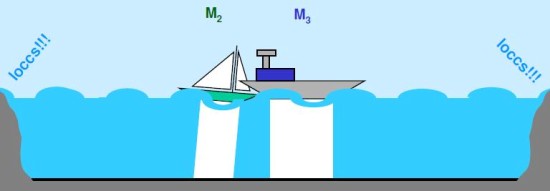
A tenger fodrozódni kezd, és a partra vetült hullámok valamiféle hatást keltenek (a tenger példánál maradva loccsanást hallunk). Lefordítva mindezt a részecskefizika nyelvére: a tenger vize a Higgs-mező, a fodrozódás maga a Higgs-részecske, a loccsanás pedig megfelel a folyamatok során keletkező és detektálható másodlagos részecskéknek. A láthatatlan elemek miatt a valóságban ezt látjuk:
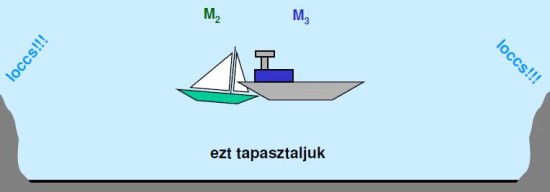
Sem a Higgs-mezőt, sem a Higgs-részecskét nem tudjuk megfigyelni, csak az általuk keltett és másként nem magyarázható másodlagos jelenségeket, a loccsanásokat (zseniális az egész hajós hasonlat, már csak ezért sem érdemes DGY előadását bármivel kiegészíteni, vagy bárhogy megváltoztatni... - a szerk.). Mindezt pedig csak igen nagy energiákon, melyek elérését az LHC (Nagy Hadronütköztető) tette lehetővé a CERN-ben.
 Összefoglalva tehát: a nyári felfedezések igazolták az elmélet helyességét és a Higgs-részecske, a Higgs-mező létezését. Utóbbi mindenütt jelen van, de változatlan, állandó háttér értékkel rendelkezik, ezért nem észlelhető. A benne mozgó részecskék a Novobátzky-képletnek megfelelően tömeghez jutnak, mely arányos a mező állandó értékével és a részecskékre jellemző – különböző – csatolási állandókkal. Maga a Higgs-részecske a mező fodrozódása, és csak másodlagos jelekből következtethetünk létezésére. Az elmélet helyre illesztette a standard modell utolsó hiányzó darabjait, és egyúttal megmagyarázta azt is, hogy a kvantum-mezőelmélet miért működik helyesen: mert a részecskéknek valóban nincs saját tömegük eredetileg.
Összefoglalva tehát: a nyári felfedezések igazolták az elmélet helyességét és a Higgs-részecske, a Higgs-mező létezését. Utóbbi mindenütt jelen van, de változatlan, állandó háttér értékkel rendelkezik, ezért nem észlelhető. A benne mozgó részecskék a Novobátzky-képletnek megfelelően tömeghez jutnak, mely arányos a mező állandó értékével és a részecskékre jellemző – különböző – csatolási állandókkal. Maga a Higgs-részecske a mező fodrozódása, és csak másodlagos jelekből következtethetünk létezésére. Az elmélet helyre illesztette a standard modell utolsó hiányzó darabjait, és egyúttal megmagyarázta azt is, hogy a kvantum-mezőelmélet miért működik helyesen: mert a részecskéknek valóban nincs saját tömegük eredetileg.
Fontos megjegyezni, hogy a Higgs-problémának nincs semmi köze a gravitációhoz, és hogy nem minden tömeg származik a Higgs-mezőtől. A proton tömegének nagy része példának okáért a benne mozgó kvarkok és gluonok mozgási energiájából adódik (részletek Katz Sándor „A látható világegyetem tömege és a részecskefizika” című előadásában).
|
Források Dávid Gyula: „A tömeg eredete és a Higgs-mező” (Az atomoktól a csillagokig előadássorozat) |
| Ha tetszett a bejegyzés, és szeretnél frissen értesülni az újakról, illetve szívesen olvasnád azokat az írásokat is, melyeket csak ajánlunk, de külön bejegyzéssé nem érnek (vagy nincs szükség kiegészítésükre), akkor csatlakozz a blog Facebook oldalához a jobb hasábban megtalálható alkalmazás segítségével! |





